행렬

행렬

수 또는 다항식 등을 직사각형 모양으로 배열한 것

ex) 1, 9, -13, 20, 5, -16을 2x3 직사각형 위에 배열한 행열은 다음과 같다

2x3 행렬

행렬의 형태

 

---

 

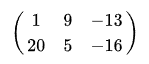
단위행렬 [ E ] (= 항등 행렬)

주대각선의 원소가 모두 1이며 나머지 원소는 모두 0인 정사각 행렬

단위 행렬

 

---

 

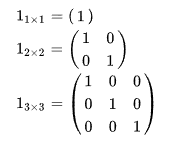
역행렬 [ A­-¹ ]

어떤 행렬 A와 곱했을 때 곱셈의 대한 항등원인 단위행렬 E가 나오게 하는 행렬을 행렬 A의 역행렬이라고 한다.

역행렬의 기호는 A­-¹라고 쓰이면 A inverse라고 읽는다.

 

일반적으로 행렬의 곱셈에 대한 성질에서는 AB ≠ BA지만 행렬과 그 역행렬 사이에는 AA⁻¹ = A⁻¹A = E 가 성립된다.

항등원과 역원에서 항등원과 역원을 가지려면 교환 법칙이 성립돼야 하는데,

 

행렬 A가 2 x 3 행렬이고, A⁻¹가 3 x 2 행렬이라면

AA⁻¹  = E가 되는데 이때 E는 2차 정사각행렬이다.

 

하지만 교환법칙에 따라 A⁻¹A = E가 될 텐데 이때 E는 3차 정사각행렬이 된다.

즉, AA⁻¹ 와 A⁻¹A 모두 단위행렬 E지만 서로 다른 행렬이 된다. 곱셈 결과가 같은 n차 단위행렬이 되기 위해선 A와 A⁻¹도 n차 정사각행렬로 되어야 한다.

 

역행렬 공식

 

---

 

전치 행렬

행과 열을 교환하여 얻는 행렬

즉, 주대각선을 축으로 하는 반사 대칭을 가하여 얻는 행렬이다

전치행렬 예시 (출처 위키피디아)

전치행렬 특징

 

---

 

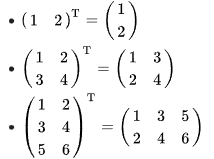
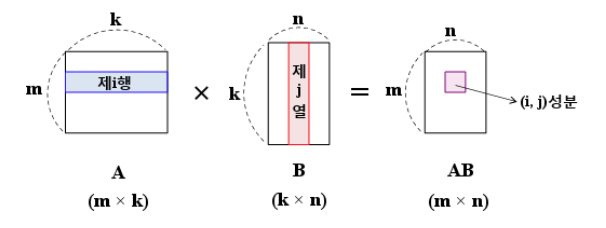
행렬의 곱연산